Simplifying Complex Fractions
Recall that a fraction can be written using the division symbol,
÷.
For example:
•
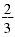 can be written 2
÷ 3. can be written 2
÷ 3.
•
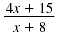 can be written (4x + 15) ÷ (x + 8).
can be written (4x + 15) ÷ (x + 8).
•
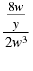 can be written can be written
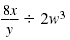
The expression,
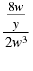 , is called a complex fraction. , is called a complex fraction.
A complex fraction is a fraction that contains other fractions.
Here are some examples of complex fractions:
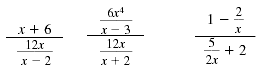
To simplify a complex fraction we first write it as a division problem.Then we follow the procedure for dividing rational expressions.
Procedure —
To Simplify a Complex Fraction
Step 1 Write the complex fraction using a division symbol,
÷.
Step 2 Invert the second fraction and change the division symbol,
, to the multiplication symbol, ·.
Step 3 Factor the numerators and denominators.
Step 4 Cancel all pairs of factors common to the numerators and
denominators.
Step 5 Multiply the numerators. Multiply the denominators.
|