Solving Systems of Equations Using Substitution
Two algebraic methods for solving systems of equations are addition and
substitution.
A “system of equations†is defined by the set of all of the lines that intersect
at the point (h, k) and the
solution which can be determined by the equations of two different lines. The simplest of these are
{ x = h, y = k } which is called the “solution set†of the system of equations. The solution is also
defined by the point of intersection: { (h, k) }.
In any system of equations (family of lines) the following are true statements.
1. A linear equation may be multiplied by a real number and form another linear equation through
the same point. (a coincident line).
2. Two intersecting linear equations may be added to form the equation of another line
through the same point on a graph.
3. One equation can be “solved for one of the variables†and that expression can then be
substituted in another equation in place of that variable.
NOTE: [Generally, use only for variables with coefficient of ±1.]
Substitution Method
Unless one of the equations is already solved for one of the variables in terms
of the other, the Substitution Method is not generally as desirable as the Addition Method.
Example 1:
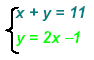
Since the second equation is already solved for y we can
use the expression on the right side as a replacement for y
in the first equation, which gives us an equation in x alone.
Solve:
| x + (2x - 1) = 11 |
Replacement for y |
| 3x - 1 = 11 |
Distributive Property |
| 3x = 12 |
Add Opps |
| x = 4 |
Multiply Recip |
Replace x = 4 in the second equation y = 2( 4 ) − 1 or y = 7.
Check: Substitute both in equation one: ( 4 ) + ( 7 ) = 11
 The solution point: { ( 4, 7) } The solution point: { ( 4, 7) }
Example 2:
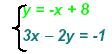
Since the first equation is already solved for y we can
use the expression on the right side as a replacement for y
in the second equation, which gives us an equation in x alone.
Substitute the expression for y in the second equation: 3x − 2(-x + 8) = − 1
Solve this equation for x:
| 3x + 2x − 16 = − 1 |
Distributive property |
| 5x = 15 |
Add Opps |
| x = 3 |
Multiply Recip |
Replace x = 3 in equation (1): y = − ( 3 ) + 8 finds y = 5 or solution point: { ( 3, 5) }
Always check in the other equation: 3(3) − 2(5) = − 1

Never consider using the substitution method if all of the coefficients
in the system are different
than ±1. If none are equal to ±1 you may have fractions to contend with and that’s just not necessary.
Some simple systems do have fractions as solutions.
In fact, if you encounter a system of equations where the coefficients are fractions, it is usually better
to multiply first by the LCM then proceed to solve the system.
|