	Algebra Tutorials!

Thursday 21st of November



	Home
	Rotating a Parabola
	Multiplying Fractions
	Finding Factors
	Miscellaneous Equations
	Mixed Numbers and Improper Fractions
	Systems of Equations in Two Variables
	Literal Numbers
	Adding and Subtracting Polynomials
	Subtracting Integers
	Simplifying Complex Fractions
	Decimals and Fractions
	Multiplying Integers
	Logarithmic Functions
	Multiplying Monomials
	Mixed
	The Square of a Binomial
	Factoring Trinomials
	The Pythagorean Theorem
	Solving Radical Equations in One Variable
	Multiplying Binomials Using the FOIL Method
	Imaginary Numbers
	Solving Quadratic Equations Using the Quadratic Formula
	Solving Quadratic Equations
	Algebra
	Order of Operations
	Dividing Complex Numbers
	Polynomials
	The Appearance of a Polynomial Equation
	Standard Form of a Line
	Positive Integral Divisors
	Dividing Fractions
	Solving Linear Systems of Equations by Elimination
	Factoring
	Multiplying and Dividing Square Roots
	Functions and Graphs
	Dividing Polynomials
	Solving Rational Equations
	Numbers
	Use of Parentheses or Brackets (The Distributive Law)
	Multiplying and Dividing by Monomials
	Solving Quadratic Equations by Graphing
	Multiplying Decimals
	Use of Parentheses or Brackets (The Distributive Law)
	Simplifying Complex Fractions 1
	Adding Fractions
	Simplifying Complex Fractions
	Solutions to Linear Equations in Two Variables
	Quadratic Expressions Completing Squares
	Dividing Radical Expressions
	Rise and Run
	Graphing Exponential Functions
	Multiplying by a Monomial
	The Cartesian Coordinate System
	Writing the Terms of a Polynomial in Descending Order
	Fractions
	Polynomials
	Quadratic Expressions
	Solving Inequalities
	Solving Rational Inequalities with a Sign Graph
	Solving Linear Equations
	Solving an Equation with Two Radical Terms
	Simplifying Rational Expressions
	Exponents
	Intercepts of a Line
	Completing the Square
	Order of Operations
	Factoring Trinomials
	Solving Linear Equations
	Solving Multi-Step Inequalities
	Solving Quadratic Equations Graphically and Algebraically
	Collecting Like Terms
	Solving Equations with Radicals and Exponents
	Percent of Change
	Powers of ten (Scientific Notation)
	Comparing Integers on a Number Line
	Solving Systems of Equations Using Substitution
	Factoring Out the Greatest Common Factor
	Families of Functions
	Monomial Factors
	Multiplying and Dividing Complex Numbers
	Properties of Exponents
	Multiplying Square Roots
	Radicals
	Adding or Subtracting Rational Expressions with Different Denominators
	Expressions with Variables as Exponents
	The Quadratic Formula
	Writing a Quadratic with Given Solutions
	Simplifying Square Roots
	Adding and Subtracting Square Roots
	Adding and Subtracting Rational Expressions
	Combining Like Radical Terms
	Solving Systems of Equations Using Substitution
	Dividing Polynomials
	Graphing Functions
	Product of a Sum and a Difference
	Solving First Degree Inequalities
	Solving Equations with Radicals and Exponents
	Roots and Powers
	Multiplying Numbers

Try the Free Math Solver or Scroll down to Tutorials!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

Literal Numbers

The “Point” of Algebra

There are a number of important advantages to developing skill in working with literal symbols to represent numbers. Among them are

(i) We can write numerical relationships very concisely. Thus, the formula

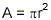
for the area of a circle is shorthand for the recipe: “to calculate the area of a circle, raise its radius value to the second power and then multiply the result by the constant 3.141592653589793 or so.” The algebraic formula makes it much easier to see the precise nature of the relationship between A and r here.

(ii) We are able to simulate arithmetic operations involving numbers whose values we don’t know at present. This makes it possible to analyze and solve all sorts of problems involving numerical values that would be impossible to solve by any other means. The rules for carrying out this arithmetic with symbols are based directly on the rules for doing arithmetic with ordinary numbers, because, after all, the symbols just represent ordinary numbers. Most of “algebra” is just learning or practicing strategies for doing this sort of symbolic arithmetic.

The development of science and technology, and most ongoing research and development work today would not be possible without an ability to represent numerical values symbolically. Skill in working with such symbolic representations is absolutely indispensable for working in nearly every technological field today.