Standard Form of a Line
If x students paid $5 each and y adults paid $7 each to attend a play for which the
ticket sales totaled $1900, then we can write the equation 5x + 7y = 1900. This
form of a linear equation is common in applications. It is called standard form.
Standard Form
The equation of a line in standard form is
Ax + By = C, where A, B, and C are real numbers with A and B not both zero.
The numbers A, B, and C in standard form can be any real numbers, but it is a
common practice to write standard form using only integers and a positive coefficient for x.
Example 1
Changing to standard form
Write the equation
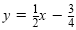 in standard form using only integers and a positive
coefficient for x.
in standard form using only integers and a positive
coefficient for x.
Solution
Use the properties of equality to get the equation in the form Ax + By = C:
| y |
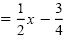 |
Original equation |
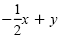 |
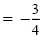 |
Subtract
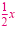 from each side. from each side.
|
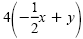 |
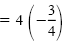 |
Multiply each side by 4 to
get integral coefficients. |
| -2x + 4y |
= -3 |
Distributive property |
| 2x - 4y |
= 3 |
Multiply by -1 to make the
coefficient of x positive. |
To find the slope and y-intercept of a line written in standard form, we convert
the equation to slope-intercept form.
Example 2
Changing to slope-intercept form
Find the slope and y-intercept of the line 3x - 2y = 5.
Solution
Solve for y to get slope-intercept form:
| 3x - 2y |
= 5 |
Original equation |
| -2y |
= -3x + 5 |
Subtract 3x from each side. |
| y |
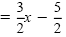 |
Divide each side by -2. |
The slope is
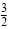 , and the y-intercept is , and the y-intercept is
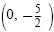 . .
Helpful Hint
Solve Ax + By = C for y, to
get
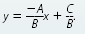
So the slope of Ax 6+ By = C is
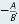 This fact can be used in
checking standard form. The
slope of 2x - 4y = 3 in Example 2 is This fact can be used in
checking standard form. The
slope of 2x - 4y = 3 in Example 2 is
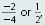 , which is the
slope of the original equation. , which is the
slope of the original equation.
|