Multiplying and Dividing Square Roots
The rules for doing arithmetic with square roots are quite
simple:
(i) multiplication:
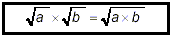 |
“the product of square roots is the
square root of the product” |
(ii) division:
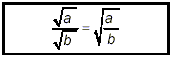 |
“the quotient of square roots is the
square root of the quotient” } |
Thus, for example:
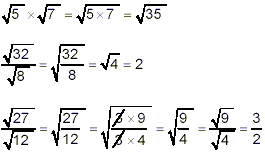
(iii) addition and subtraction: There is NO simple
relationship between the square roots of a sum or a difference
and the square roots of its terms. In particular, in symbols,
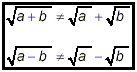
You need to use algebraic methods to demonstrate why these
prohibitions apply. However, it is possible to see the problem
using a simple numerical example.
Note that
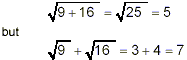
Thus 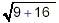 does not give the same
value as does not give the same
value as 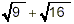 . That is: . That is:
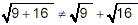
Since the two forms are unequal in this specific example, we
have demonstrated that you cannot rely on 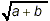 to be equivalent to to be equivalent to 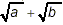 . (In fact, these two
forms are only equivalent in the relatively uninteresting cases
where a or b or both are equal to zero!) . (In fact, these two
forms are only equivalent in the relatively uninteresting cases
where a or b or both are equal to zero!)
Similarly,
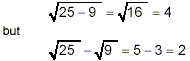
which demonstrates that
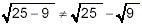
NOTE: The rules described above for doing
arithmetic with square roots also apply to any other order of
roots (cube roots, fourth roots, etc.) as long as all of the
roots have the same order. So, for example,
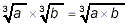
and so on.
|