The Cartesian Coordinate System
Suppose we know the sum of two numbers is 6.
We can represent this situation with the equation x + y = 6.
There infinitely many possibilities for x and y. For example:
| 1 and 5 1 + 5 = 6 |
-4 and 10 -4 + 10 = 6 |
0 and 6 0 + 6 = 6 |
We can visualize this relationship between x and y using two number lines,
one for x and the other for y.
First, draw a horizontal number line.
This is usually called the x-axis and is labeled with the variable x.

Next, draw a vertical number line perpendicular to the x-axis.
The two number lines should intersect at their zeros.
The vertical number line is usually called the y-axis and is labeled with the
variable y.
The point of intersection, the zero of each number line, is called the origin.
To make it easier to locate a point, we draw a rectangular grid as a
background.
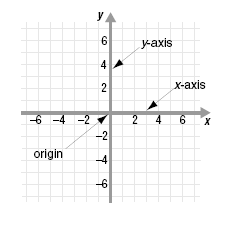
The axes and the grid define a flat surface called the xy-plane.
The number lines and grid form a rectangular coordinate system. We
typically use x and y for the variables, so a rectangular coordinate system
is often called an xy-coordinate system. The French mathematician Rene
Descartes (1596-1650) is credited with developing this type of coordinate
system, so it is also referred to as the Cartesian coordinate system.
The x- and y-axes divide the plane into four regions called quadrants. We
label these with Roman numerals I, II, III, and IV in a counter-clockwise
direction beginning in the upper right.
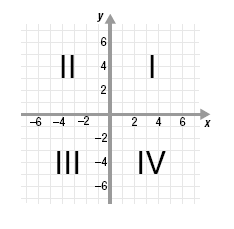
| Quadrant
I
II
III
IV |
Sign of x
positive
negative
negative
positive |
Sign of y positive
positive
negative
negative |
A point on an axis does not lie in a quadrant.
Example 1
State the quadrant in which each labeled point lies.
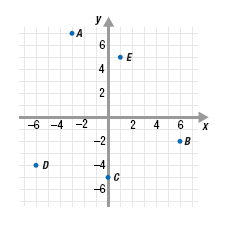
Solution
a. Quadrant II. Point A lies in the upper left quadrant.
b. Quadrant IV. Point B lies in the lower right quadrant.
c. None. Points on either axis do not lie in a quadrant.
d. Quadrant III. Point D lies in the lower left quadrant.
e. Quadrant I. Point E lies in the upper right quadrant.
|