Miscellaneous Equations
The following examples shows an equation that is not originally in the form of
a quadratic equation. However, after simplifying this equation, we get a quadratic
equation.
Even though completing the square can be used on any quadratic equation,
factoring and the square root property are usually easier and we can use them when
applicable. In the next example we will use the most appropriate method.
Example
An equation containing a radical
Solve
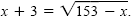
Solution
Square both sides of the equation to eliminate the radical:
| x + 3 |
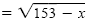 |
The original equation |
| (x + 3)2 |
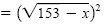 |
Square each side. |
| x2 + 6x + 9 |
153 - x |
Simplify. |
| x2 + 7x - 144 |
= 0 |
|
| (x - 9)(x + 16) |
= 0 |
Factor. |
| x - 9 = 0 |
or |
x + 16 |
= 0 |
Zero factor property |
| x = 9 |
or |
x |
= -16 |
|
Because we squared each side of the original equation, we must check for extraneous
roots. Let x = 9 in the original equation:
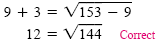
Let x = -16 in the original equation:
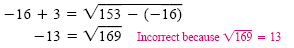
Because -16 is an extraneous root, the solution set is {9}.
|