Solving Equations with Radicals and Exponents
Raising Each Side to a Power
Example 1
Raising each side to a power to eliminate radicals
Solve each equation.
a)
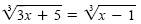
b)
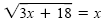
a)
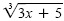 |
 |
Original equation |
 |
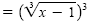 |
Cube each side. |
| 3x + 5 |
= x - 1 |
|
| 2x |
= -6 |
|
| x |
= -3 |
|
Check x = -3 in the original equation:
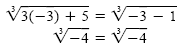
Note that
 is a real number. The solution set is
{-3}. In this example we
checked for arithmetic mistakes. There was no possibility of extraneous solutions
here because we raised each side to an odd power. is a real number. The solution set is
{-3}. In this example we
checked for arithmetic mistakes. There was no possibility of extraneous solutions
here because we raised each side to an odd power.
b)
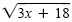 |
= x |
|
|
|
Original equation |
| 3x + 18 |
= x2 |
|
|
|
Square both sides. |
| -x2 + 3x + 18 |
= x2 |
|
|
|
Simplify. |
| x2 - 3x - 18 |
= 0 |
|
|
|
Subtract x2 from each side
to get zero on one side. |
| (x - 6)(x + 3) |
= 0 |
|
|
|
Multiply each side by -1 for easier factoring. |
| x - 6 |
= 0 |
|
|
|
Factor. |
| x |
= 0 |
or |
x + 3 |
= 0 |
Zero factor property |
| |
= 6 |
or |
x |
= -3 |
|
Because we squared both sides, we must check for extraneous solutions. If x
= -3
in the original equation
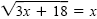 , we get , we get
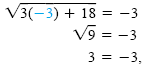
which is not correct. If x = 6 in the original equation, we get
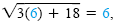 which is correct. The solution set is
{6}. which is correct. The solution set is
{6}.
|