Rotating a Parabola
Sketch the graph of
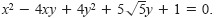
Solution
Because A = 1, B = -4, and C = 4, you have

The trigonometric identity 2θ = (cot2
θ - 1)/(2 cot θ) produces
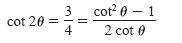
from which you can obtain the equation

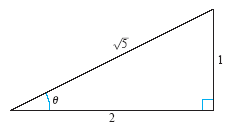
Considering 0 < θ < π/2, it follows that
2 cot θ = 4. Thus,

From the triangle in the figure below, you can obtain
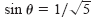 and and
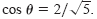
Consequently, you can write the following.
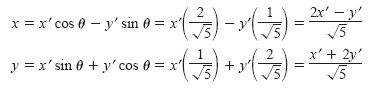
Substituting these expressions into the original equation produces
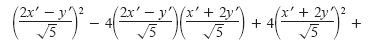 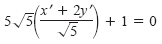
which simplifies to
5(y')2 + 5x' + 10y' + 1 = 0
By completing the square, you can obtain the standard form
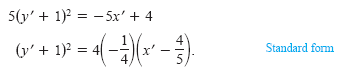
The graph of the equation is a parabola with its vertex at
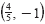 and its axis parallel
to the x'-axis in the y'-system, as shown in the figure below. and its axis parallel
to the x'-axis in the y'-system, as shown in the figure below.
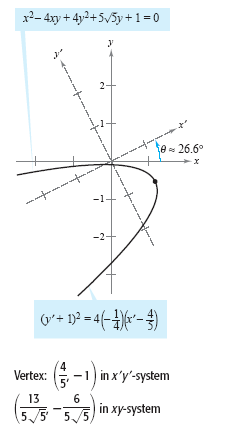
|